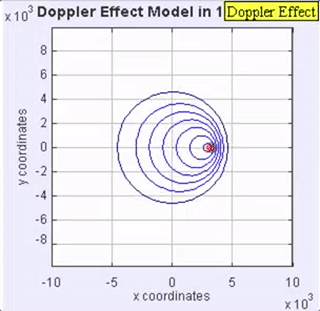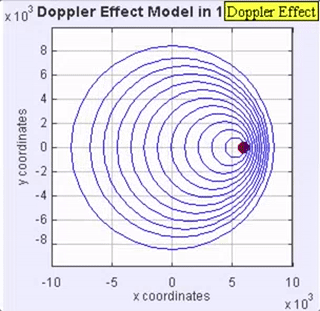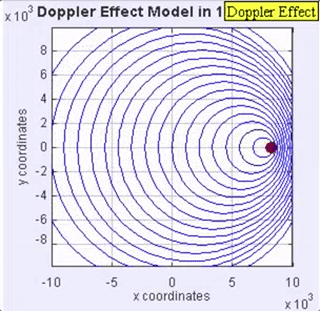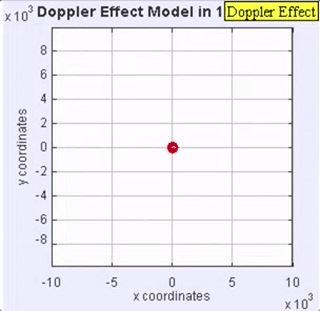
The doppler effect is caused when a light source is moving relative to the viewer.

As seen in the GIF, as the source produces waves it moves towards waves it has already produced, resulting in a squishing effect which increases the frequency to a viewer that the source is heading towards, and decreases if the source is moving away from the observer. This becomes very easy to calculate when we are directly in the line of sight of the source’s velocity. I was going to skip the derivation, but I just realized I’ve never done it and will now try my hand at it, I am going to just assume the wave moves at the speed of light in a vacuum \(c\):
Lets think about wave sources that produce a peak every \(\tau\) or have a frequency of \(1/\tau = \nu_0\). Lets assume a moving observer at \(v_{obs}\) and moving source \(v_{src}\) (both at non relativistic speeds, see relativity). We can say that the observer thinks it is stationary and sees the observer going at \(v_{src}' = v_{src} - v_{obs}\) and \(c' = c - v_{obs}\). Now we can use the \('\) versions and just pretend that the observer is stationary.
Lets first see that \(c = \lambda_0
\nu_0\) If the source starts at \(x=0\) and \(t=0\) is when wave front 1 is produced and
since we have a frequency of \(\nu_0\)
the next wave front is produced at \(t=1/\nu_0\).
\[
\begin{gather*}
x_{f1}(t)
\Rightarrow x_{f1}(\tau) = c' \tau \\
x_{f2}(t)
\Rightarrow x_{f2}(\tau) = v_{src}' \tau \\
\end{gather*}
\]
The difference between the wave fronts is the wavelength \(\lambda\) (not to be confused with \(\lambda_0\) which is the wavelength of the source waves).
\[ \begin{align} c' &= \lambda \nu \\ \lambda &= x_{f1}(\tau) - x_{f2}(\tau) \\ c'/\nu &= c' \tau - v_{src}' \tau \\ c'/\nu &= (c' - v_{src}') / \nu_0 \\ \nu &= \nu_0 \frac{c'}{c' - v_{src}} \\ \nu &= \nu_0 \frac{c - v_{obs}}{c - v_{obs} - v_{src} + v_{obs}} \\ \nu &= \nu_0 \frac{c - v_{obs}}{c- v_{src}} \end{align} \]
In reality this means a lot to us for a lot of reasons, seeing as how light is rather important. Since the doppler effect depends on the speeds of objects, we can use it (possibly unsurprisingly) to measure speeds of things that produce and reflect light.
One famous example of this is the discovery that the universe is expanding. We were able to determine this by observing that most galaxies were more red than we expected them to be, and red-shifted light (lower frequency) means they were moving away from us.
Of course at slower speeds we will not be able to measure the difference. If we assume out detector (observer) is not moving our (non relativistic) doppler equation becomes: \[\nu = \nu_0 \frac{c}{c- v_{src}}\] which means our source needs to be moving really fast in order to cause a significant difference in frequency.
The way we can measure slow speeds is by measuring something called the beat frequency. If you have ever heard a “whaaa whaaa whaaa” when two sounds have a similar frequency, thats likely a beat frequency caused by interference. I am not going to derive it here but a beat frequency \(\nu_{beat} = |\nu_1 - \nu_2|\) is easy to detect when the two frequencies are close. That means if we have a laser at some frequency \(\nu_0\) and alter that frequency a bit (possible by using the doppler effect bounding off a slow moving object…) then we can create a beat frequency that is in the measurable range. Of course to do this we have to know the original frequency of the light, but we can generally assume we know the frequency of a laser that we buy so looks like we are all set, now all we have to do is set of a geometry so the laser and the doppler shifted light both hit the detector.
So using what we know, we can come up for an equation to find the speed of a moving train given the beat frequency produced by the original laser and its doppler shifted reflection: \[ \begin{align*} ν_{beat} &= |ν_0 - ν_{final}| \\ ν_{final} &= \frac{c + v_{train}}{c- v_{train}} \nu_0 \\ ν_{final} (c- v_{train}) &= \nu_0 (c + v_{train}) \\ ν_{final} c - ν_{final} v_{train} &= \nu_0 c + \nu_0 v_{train} \\ ν_{final} c - \nu_0 c &= \nu_0 v_{train} + ν_{final} v_{train} \\ \frac{ν_{final} c - \nu_0 c}{\nu_0 + ν_{final}} &= v_{train} \\ \frac{(\nu_0 + \nu_{beat}) c - \nu_0 c}{\nu_0 + (\nu_0 + \nu_{beat})} &= v_{train} \\ c \frac{\nu_{beat}}{2\nu_0 + \nu_{beat}} &= v_{train} \end{align*} \]
It is important to notice what values have error here. I took many measurements of \(\nu_{beat}\) and got a value of \(460 \pm 20 \text{ kHz}\) where the uncertainty is statistical uncertainty. The laser comes with a bandwidth of what the actual frequency is going to be. The value from the manufacturer is \((4.73611764 \pm 0.00000002) \times 10^{14}\text{ Hz}\) but I am going to double check and to keep it interesting let me use \((4.74 \pm 0.01) \times 10^{14}\text{ Hz}\). After error-propagation I get: \[ \begin{gather*} f(x_1, x_2, ..., x_n) \\ \Rightarrow \sigma_f(x_1,\sigma_{x_1}, x_2,\sigma_{x_2}...,x_n,\sigma_{x_n}) \\ = \sqrt{(\frac{\partial f}{\partial x_1}\sigma_{x_1})^2 + ... + (\frac{\partial f}{\partial x_n}\sigma_{x_n})^2} \end{gather*} \\ \Rightarrow\sigma_{v_{train}}= \sqrt{(\frac{c}{\nu_{beat}+2\nu_0})^2} \\ = \sqrt{\frac{4 \sigma_{f_0}^{2} c^{2} f_{b}^{2}}{\left(2 f_{0} + f_{b}\right)^{4}} + \sigma_{f_beat}^{2} \left(- \frac{c f_{b}}{\left(2 f_{0} + f_{b}\right)^{2}} + \frac{c}{2 f_{0} + f_{b}}\right)^{2}} \] The value for v_train is 0.146e +/- 0.006 m/s m/s.